["라오어 미국주식 무한 매수법"이 효과적인 종목에 대한 수학적 고찰]

먼저 난 주린이며 재테크 초보다. 그리고 공돌이다.

나는 "라오어의 미국주식 무한 매수법" 이라는 책을 읽고 이 책에 나오는 매매 방법으로 수익인증을 하는 수많은 사람들을 보며 나도 이 매매방법에 뛰어 들었다.

http://www.kyobobook.co.kr/product/detailViewKor.laf?mallGb=KOR&ejkGb=KOR&barcode=9791165795788#review

"라오어의 무한 매수법"의 기본 원리는 변동성이 큰 레버리지 종목을 이용하여 하락장에서 매일 분할매수를 하여 평단을 계속 낮췄다가 가격이 평단의 10%이상을 넘어가면 보유수량을 모두 매수하여 수익을 실현하는 방법이다. 자세한 방법은 아래와 같다.

• 원금설정 및 분할기간 설정
  1. 원금을 40분할로 나누고 절대로 다른 곳에 사용하지 않는다.
     1. 40분할된 (1/40) 금액→매수시도액
  2. 하루 “매수시도액”으로 최소 2주를 살 수 있는 종목을 선정
  3. 여러 종목을 할 경우 종목마다 원금을 분리하고 절대 섞지 않는다.
• 매수는 매일 걸어 둠
  1. 첫 번째 매수는 장중 아무 시간에 한 주를 매수한다.
     1. 두 번째 매수부터는 LOC 매수로 매일 “최대 1회”(매수시도액으로 최대로 살 수 있는 양 $n_{max}$ 주를) 매수한다.
     2. 하루 매수 시도액의 절반(0.5회)(LOC 평단 매수): 현재 평단가로 매수 주문을 걸어 놓음
     3. 나머지 절반(0.5회)(LOC큰수매수): LOC 매수로 평단가보다 10~15% 위쯤에 걸고 잠을 잠
     4. 주의할점: 어제 0.5회를 매수했다고 해서 오늘은 1.5(=1.0+0.5) 회 매수하면 안됨. 하루 최대 1회 매수임!!
  2. 만약 장 중 가격이 이미 내 평단가보다 낮을 경우 장중에 1회분량을 모두 실시간 매수해도 된다.
  3. 주가 하락 상승에 의해 매수 수량이 변할 수 있음 (무한 매수법은 “정액법”임 정량법이 아님)
• 매도도 매일 걸어 둠
  1. 매도는 지정가 (현재 내 평단 대비 10% 높은 수익지점)에 보유 주식 모두 지정가 매도를 걸면됨
     1. 프리장에 지정가 매도를 걸어두면 본장이 끝날 떄까지 주문이 유지된다.
     2. 만약 정해진 원금을 모두 소진할 때까지 위 방법으로 매도가 되지 않는다면 “무한매수법 영혼법”으로 이동!

“무한매수법 영혼법”

1. 원금 소진후 수익률 -10~+10%: 그냥 모두 매도하고 리셋후 무한매수법 다시 시작
2. 원금 소진후 수익률 < -10%:
   1. 기존 계좌는 매수도 매도도 하지 않고 정지
   2. 새로운 계좌를 개설후 1회차 매수부터 무한매수법 다시 시작
   3. 새로운 계좌에서 +10% 매도수익이 발생하면 기존계좌에서 그 수익금만큼 손해금이 나오도록 매도한다.
   4. 손해를 만회하면 새 계좌 처분 후 다시 기존계좌로 무한매수법 이어나가면 됨.

 

 

이 책의 지은이 라오어님은 이 무한매수법을 개발하신 분이고 계속해서 방법을 업그레이드하고 계신다. 라오어님이 운영하는 네이버 카페도 존재한다. 이 카페는 라오어님이 계속 업그레이드 하는 방법들도 다 공개가 되어 있다. 이런 매수법은 매일매일 매매를 진행해야하므로 수동보다는 자동매매프로그램을 만들어서 하는게 효과적이다(본인도 파이썬 기반의 프로그램을 만들어서 사용중이다)

내가 뛰어든 시기는 40일 전이다 (어제의 매매로 40일째 매매다). 난 업그레이드된 버젼 말고 가장 초기 버젼의 무한매수법을 시행하고 있고 현재 수익률이 마이너스다. 라오어님 유튜브에서 봤는데 지금은 모두 하락장이라서 라오어님께서도 현재 무한매수법 수익률이 계속 마이너스인듯 하다.

나도 아주 기본적인 원리 만 대략이해하고 바로 뛰어들었지만 수익률이 마이너스라서 그런가 내가 너무 얕게 이해하고 있는게 아닌가 라는 생각이 들면서 갑자기 무한매수법에 대해 좀더 수학적으로 이해하고 싶어졌다. 공대생의 본능인가보다.

서론이 길었다. 오늘의 주제는 "무한매수법이 효과적인 종목에 대한 수학적 고찰"이다.

다음과 같은것을 하였다

1. 무매법을 하는 종목의 수학적 모델링
2. 종목의 특징을 나타내는 파라미터(레버리지수, x1인덱스 종목의 변동성, 모멘텀유지력) 를 이것저것 변경하면서 어떤 종목에서 무한매수법이 유리한지 분석

 

종목 수학적 모델링

수학적 모델링에 앞서 아주 강한 가정을 통해 매우 간단한 수학적 모델을 만들었기 때문에 실제 종목의 동작과 많이 다를 수 있음을 미리 말해두고싶다

먼저 무한매수법을 하는 종목의 레버리지 x1 에 해당하는 종목은 장기적으로 무조건 우상향한다는 가정을 하여 평균적으로는 하루에 $\bar{\alpha}$ 배 만큼 가격이 상승한다고 가정하자. 그러면 $k$번째 날에 등락률을 $r_k$라고 하였을때 (등락률의 변동성이 충분히 작다면)다음과 같이 나타낼 수 있다.

$\mathbb{E}[\alpha_k = \log{(1+r_k)}]=\bar{\alpha}$ 

$r_{k}$는 다음과 같은 확률 분포를 따른다고 가정하자

$\alpha_0=\log{(1+r_0)} \sim P_{rate}(\cdot ;\bar{\alpha}, \sigma ) \mathcal{N}(\cdot |\bar{\alpha},\sigma^2)$

 

$P(\alpha_{k+1}|\alpha_k<0) =(1-p_1)P_{right}(\cdot ;\bar{\alpha}, \sigma ) + (p_1)P_{left}(\cdot ;\bar{\alpha}, \sigma )$

 

$P(\alpha_{k+1}|\alpha_k\ge 0) = (p_1)P_{right}(\cdot ;\bar{\alpha}, \sigma ) + (1-p_1)P_{left}(\cdot ;\bar{\alpha}, \sigma )$

여기서

$P_{right}(\cdot ;\bar{\alpha}, \sigma )$는 확률밀도함수$P_{rate}(\cdot ;\bar{\alpha}, \sigma ) $의   $\alpha$가 양수인 부분에 몰빵한 확률밀도 함수($\alpha$가 음수일때는 0)다

($P_{left}(\cdot ;\bar{\alpha}, \sigma )$도 비슷하게 $\alpha$가 양수인 부분에 몰빵한 함수)

일종의 $r_k$에 대한 Markov process가 만들어진 셈이다. 이렇게 되면 임의의 $k$에 대해서 다음을 만족하게 되어

$\alpha_k \sim P_{rate}(\cdot ;\bar{\alpha}, \sigma )$

여전히 레버리지 x1 종목은 장기적으로 우상향하게 된다.(구체적 유도과정은 생략)

 

$\alpha_k=\log{(1+r_k)} \sim P_{rate}(\cdot ;\bar{\alpha}, \sigma ) \mathcal{N}(\cdot |\bar{\alpha},\sigma^2)$

 

자, 이제 이 등락률 Markov process를 이용해서 무한매수법을 진행하는 시뮬레이션을 진행해보고 결과를 보자!

 

이제 무한 매수법 규칙을 적용하여 더 큰차원의 state로 이루어진 Markov process를 만들고 시뮬레이션을 진행하면된다.

시뮬레이션 모델을 더 간단하게 만들기 위해서 실제 무한 매수법의 기본원리는 지키면서도 규칙을 좀더 단순화한 무한매수법을 적용하였다(매일 1회차 양만큼 무조건 매수를한다, 매수는 시장이 열릴때, 매도는 시장이 닫힐때 한다, 수량은 모든 양의 실수가 가능하다)

state는 하루 등락률 $r_k$, 1주 가격 $Q_k$, 평단 $D_k$, 레버리지 x3 종목 보유수량 $M_k$, 현금 보유수량 $C_k$ 가 되겠다. State transition 에 대한 수식은 아래와 같다

 

$Q_{k+1} = Q_k(1+N_{lev}r_s)$ 

 

$D_{k+1} = Q_{k+1}$  if   $Q_{k+1} > (1+r_s)D_k$

$D_{k+1} = \frac{D_kM_k+q}{M_k+\frac{q}{Q_{k+1}}}$  else

 

$M_{k+1}=q/Q_{k+1}$  if   $Q_{k+1} > (1+r_s)D_k$

$M_{k+1}=M_k+\frac{q}{Q_{k+1}}$   else

 

$C_{k+1}=C_k + Q_{k+1}M_k - q$  if   $Q_{k+1} > (1+r_s)D_k$

$C_{k+1} = C_k-q$    else   

 

여기서 $q$는 1회차 매수시도액이고 $r_s$는 매도 기준이 되는 평단대비 등락률(=0.1=10%)이고 $N_{lev}$는 레버리지 배수(x3)이  되겠다

 

 

 

시뮬레이션 결과

시뮬레이션 상에서 바꿔볼 파라미터는 $\sigma$ 와 $p_1$ 이다. $\sigma$는 레버리지 x1 종목의 등락률의 변동성을 의미하고 $p_1$은 해당 종목의 모멘텀 유지력을 나타낸다고 볼 수 있다.

결과는 다음과 같다

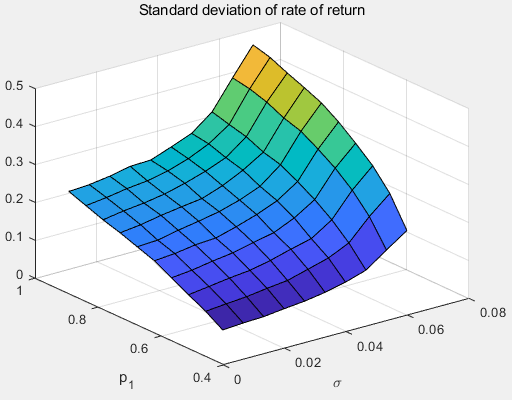
위 그래프는 파라미터 세트 하나당 총 10000번의 시도를 하여 각 파라미터 세트의 한 싸이클 평균 수익률, 한 싸이클 수익률의 표준편차(수익률 변동성)을 나타낸 것이다. 

 

그래프로 표현은 안했지만 $N_{lev}$의 값을 높일 수록 수익률이 높아지는 결과로 보아 레버리지의 수익성은 시뮬레이션 결과로도 입증이 된 셈이다. 하지만 이 결과에서 조금 이상한점은 $\sigma$가 클수록 변동성이 큰것이고, 라오어님의 말씀에 따르면 더 수익률이 커야되는데 시뮬레이션 결과는 정 반대다. 이는 일단 라오어님의 말씀이 틀린것이 아니라 내가 모델링한 종목모델이 현실과  괴리가 있어서인 것으로 분석된다. 특히 앞서 설명한 부분중에

$\alpha_k=\log{(1+r_k)} \sim P_{rate}(\cdot ;\bar{\alpha}, \sigma ) \mathcal{N}(\cdot |\bar{\alpha},\sigma^2)$

이부분이 사실 실제 시장과 괴리가 꽤 있다. $\sigma$가 극단적으로 작다고 가정 했을때 $r$은 음수일때는 거의 0에 가까운 값만 가질 수 밖에 없게 돼서 $Q$가 매시간 거의 단조 증가함수처럼 극단적으로 우상향할수 밖에 없기 때문에 나타나는 현상인 듯하다. 따라서 $\sigma$가 작을수록 수익률이 높아질 수 밖에 없다. 

 

또한가지 주목할점은 모멘텀 유지력 $p_1$이 커질 수록 무한매수법으로 얻는 수익률이 낮아 진다는 것이다. 즉 가격이 오랜 기간동안 계속 증가하거나 가격이 계속 하락하는 장 (지금 같은 시기)에서는 무한매수법은 빛을 보지 못한다는 것을 분석할 수 있었다.

 

수익률의 변동성도 주목해야할 수치다. 수익률의 변동성의 경우 $p_1$이 커질수록 $\sigma$가 커질 수록 증가한다.

 

모멘텀 유지력이 큰 종목일 수록 (혹은 시장의 모멘텀 유지력이 전체적으로 큰 기간동안은) 무한매수법의 수익률도 낮고 수익률의 변동성도 커서 빛을 보기 어렵다.

 

따라서 모멘텀 유지력이 작은 시장에서 무한매수법이 잘 작동함을 알 수 있다!

이를 통해 모멘텀 유지력이 긴 기간동안을 대응하는 기술을 개발하여 라어어의 무한매수법을 업그레이드 할 수 있는 방안도 생각할 수 있을 것 같다!